KISSING COINS
By Rachel Van Kopp, Kimberly Younger, Tracy Van Lone, Natasha Smith, and Naomi Johnson
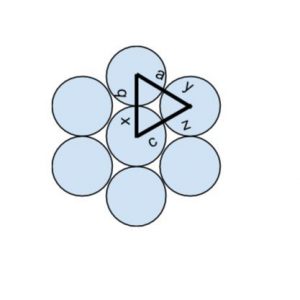
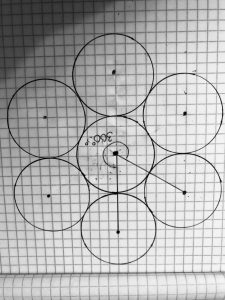
7 chips are arranged to kiss (touch) each other.
The chips are connected to each other and look similar to a flower.
What if the coins were different sizes?
The chips are still connected in the same pattern.
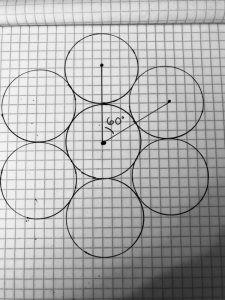
After sketching a picture including all seven chips it quickly becomes a parent that there are 6 lines of symmetry. 3 of the lines of symmetry go through the center of two circles. after connecting all of the circles’ center points it is easy to see 6 triangles and 1 hexagon.
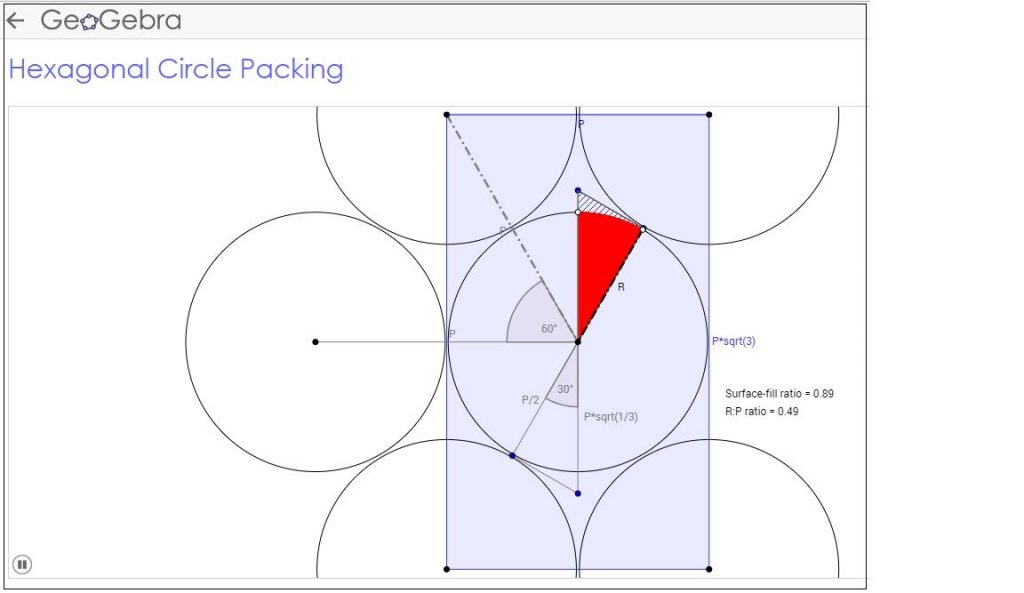
Proof – That the radius of the center circle is equal to the six outside circles. The proof is below.
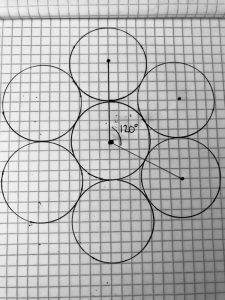
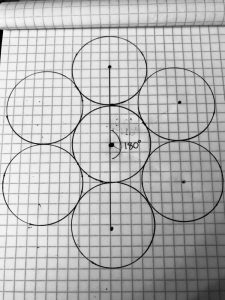
The connection between circles, triangles, and regular polygons is an important part of why the circles of all the same sizes touch. The proof shows that the center points of 3 circles will create a triangle with a 60 degree angle. If you add on an additional circle your angle will be 120 degrees. Add another circle and the angle will be 180 degrees, add another circle and the angle will be 240 degrees, and adding another circle will be 300 degrees. The proof is related to the standard CCSS.CONTENT.MATH.8.G.A.5 because the standard is discussing equilateral triangles and the cos proof we used is based off of an equilateral triangle.
Extension:
Teachers can expand on sphere packing and what the packing number would be at different dimensions, i.e. how many spheres in a 3D packed space. Teachers can expand with unequal sphere packing, which would be spheres with different radii. Or another extensions could be adding layers onto the original circles and figuring out how many circles will fit on the third or fourth layer
(Follow this link to the video.)
Click the image below to watch a GeoGebra Video about Hexagonal Circle Packing.