Learning Progression edTPA
High School: Algebra with Trigonometry
EXPONENTIAL GROWTH AND DECAY
The class I will be teaching is an algebra class with
trigonometry. The textbook used will be Algebra 2:
Equations, Graphs, applications by Ron Larson, Laurie
Boswell, Timothy D. Kanold, and Lee Stiff, published 2004
by McDougal Littell. This learning progression will follow
the student through meeting the Common Core State
Standards about exponential growth and decay. These
Common Core State Standards will be covered in chapter
8 of the textbook, sections 1 and 2. These sections cover
exponential growth and decay models. That is, to be able
to create an equation, graph it, and solve problems with
exponential models. The standards for these lessons will
cover the cluster involving exponential functions,
including HSF.LE.A.1.C, HSF.LE.A.3, and HSF. LE.B.5. The
math practices that are going to be used throughout the
learning progression are as follows: MP2, MP3 and MP4.
These lessons will span three days. The exponential
growth model lessons will take the first two days and the
exponential decay model lesson will take the third day.
On the fourth day, the students will have a worksheet
with practice problems covering 8.1 and 8.2. This gives
the students a chance to show me how well they are
understanding the material because I will collect the
worksheet at the end of class and will use it to see how
the students are doing. I can assess what they
understand and what I need to cover again.
CCSS.Math.Content.HSF.LE.A.1.C:
which is about modeling exponential
functions and interpreting situations that
need to be solved with an exponential model.
CCSS.Math.Content.HSF.LE.A.3:
Observe using graphs and tables that a
quantity increasing exponentially eventually
exceeds a quantity increasing linearly,
quadratically, or (more generally) as a
polynomial function.
CCSS.Math.Content.HSF.LE.B.5
Interpret the parameters in a linear or
exponential function in terms of a context.
COMMON CORE STATE STANDARDS
MATHEMATICAL PRACTICES
CCSS.Math.Practice.MP2:
Reason abstractly and quantitatively
CCSS.Math.Practice.MP3:
Construct viable arguments and critique the
reasoning of others.
CCSS.Math.Practice.MP4:
Model with mathematics.
Lesson 8.1 Exponential Growth Day 1
This lesson is the first day of a two-day lesson on
exponential growth model. Day-one is an introductory
lesson to the concept. I will start the lesson off by asking the
students what they remember from the prior year about
exponential growth. The students would have been
introduced to the concept in their algebra 1 course with a
very basic overview of the concept. I will then give the
students the equation for exponential growth for them to
get in their notes. The equation is y=bx where b>1 to create
a growth equation. I will tell the students that if the b is less
than 1 this is a decay function which we will get to later in
the chapter. I will also define an asymptote as it relates to
the graph, that is a horizontal asymptote on the x-axis or
y=0. I will then give the students four example problems in
which we will go through graphing together. Once I will as
though the students understand how to graph exponential
growth, I will show them a more complex equation which
includes transformations. They will now have the equation
y=abx-h+k where a represents stretching and shrinking, h is
the shift left or right and k is the shift up and down. I will
then give the students one equation to graph on their own
using transformations.
After we have completed the notes for this section, I will
move to a class activity. I will post graph paper sticky notes
on the front board with exponential equations on the top of
each paper. The students will come to the front of the class
and pick a sticky note and graph it individually, which is
modeling or MP4. They will put their names on the back and
post them back on the board when they are finished. They
will then look over other answers that have been posted. If
the students have and questions or comments, they can
look at the name on the back and find the person to discuss
the answer. The students will then have to explain their
answer and their thinking which will create great
conversations about the concepts, thus using MP3 in this
activity.
Learning Targets:
I know about the exponential growth
model.
I can graph exponential growth
equations
Common Core State Standard:
CCSS.Math.Content.HSF.LE.A.1.C:
which is about modeling exponential
functions and interpreting situations
that need to be solved with an
exponential model.
CCSS.Math.Content.HSF.LE.A.3:
Observe using graphs and tables that a
quantity increasing exponentially
eventually exceeds a quantity increasing
linearly, quadratically, or (more
generally) as a polynomial function.
CCSS.Math.Practice.MP3:
Construct viable arguments and critique
the reasoning of others.
CCSS.Math.Practice.MP4:
Model with mathematics.
Lesson 8.1 Exponential Growth Models Day 2
This lesson is the second day of exponential growth model.
On day two, we will be working with applying the growth
model to word problems. I will be giving the students a new
formula they can use for application problems to create a
function as it relates to each word problem. The new growth
model is y=a(1+r)t where a is the initial amount, r is the
growth percentage as a decimal, t is the time, and y is the
end amount. I will also explain to the students that the
quantity (1+r) is known as the growth factor. After discussing
these notes, we will move to example problems to apply the
concepts. I will give the students a word problem and have
them tell me what information goes where in the formula.
Then once we have created a function, I will have them
graph it and have them solve for an end amount after a
given time. We will do this again with another problem to
practice. I will then ask the students how they are feeling
about the material by giving me a thumbs-up, thumbs-down,
or thumbs-sideways depending on how they feel. If the
students still seem to struggle with the concept, we will go
over another problem. If the students are understanding the
concepts then we will move to an activity.
For the activity for this lesson, I will write five different
exponential growth model functions on the board. The students
will choose one then graph the function and create a real-world
problem from the equation. The students will need to come up
with a scenario that will match the function. This will use MP4 for
the graphing and modeling and MP2 for reasoning abstractly and
creating a scenario from the equation. Once the students have
their scenario, they will share their word problem with their
neighbor and the neighbor must guess which function matches
the scenario. For example, student 1 and student 2 are paired up.
The students swap scenarios with the function covered or hidden.
Student 1 must guess which function student 2 choose and
explain their thinking, then they will repeat this with student 1’s
scenario. If either of them gets it wrong, they must guess again.
This gives the students a chance to show their understanding or
where they struggle. The students can help each other verify if
their answers are right and create great mathematic
conversations about exponential growth models.
Learning Targets:
I know about the exponential growth
model.
I can use the model to solve application
problems.
Common Core State Standard:
CCSS.Math.Content.HSF.LE.A.1.C:
which is about modeling exponential
functions and interpreting situations
that need to be solved with an
exponential model.
CCSS.Math.Content.HSF.LE.B.5
Interpret the parameters in a linear or
exponential function in terms of a
context.
CCSS.Math.Practice.MP2:
Reason abstractly and quantitatively
CCSS.Math.Practice.MP4:
Model with mathematics.
Lesson 8.2 Exponential Decay
For the final lesson in this learning progression, we will be
covering exponential decay. I will remind the students about
when I briefly mentioned how decay relates to growth on
the first day. I will ask the students to remind me of the
exponential function we used on the first day with the
transformations, which is y=ab(x-h)+k. I will then ask the
students to define each term in their own words. This gives
me a chance to assess whether or not the students were
taking notes and understanding the material. By having
them put it in their own words, it forces the students to
show an understanding of the concept rather than just
reading from their notes. I will also remind them that for the
function to be a decay model rather than a growth model,
the b value must be between 0 and 1. If the b value is above
1, we will have an exponential growth model. I will also
discuss the long term for the graph, as the t value gets large,
then the end amount or y value will get closer and closer to
zero but will never be zero, therefore having an asymptote
at y=0 or the x-axis. As long as the students do not have any
questions about this equation, we will move onto doing
some practice problems of graphing three different
functions with the same b value of ½ but each has different
transformations.
Once we are done graphing each example, I will ask the
students to remind me of the exponential growth model
they had learned the day before, which was y=a(1+r)t. For
decay the equation is nearly the same except the growth
factor is now a decay factor and is 1-r instead of 1+r,
therefore making the quantity less than 1. All the terms are
the same as in the growth model, however the r value is
now a decay rate as a decimal instead of a growth rate.
Thus, the decay model being y=a(1-r)t.
After comparing the growth model to the decay model, I will
give the students a class activity. I will give the students a
word problem to apply the decay model to. This will be a
three-part problem where they will write the decay model
based on the problem, then graph the model, and finally solve for the end value after 3 years.
Students will work on this individually then discuss it with their neighbor once most people are
done. Once everybody seems to be done discussing the problem, I will give them the answer to
the end value after three years to check their work. If they got this correct then their decay
model should be correct and they should be able to find this point on their graph is they look at
what the value of y is when x is 3. This allows the students to check their work without me
going over each part and giving them all the answers.
Learning Targets:
I can graph the exponential decay
function.
I can solve problems using the
exponential decay functions.
Common Core State Standard:
CCSS.Math.Content.HSF.LE.A.1.C:
which is about modeling exponential
functions and interpreting situations
that need to be solved with an
exponential model.
CCSS.Math.Content.HSF.LE.A.3:
Observe using graphs and tables that a
quantity increasing exponentially
eventually exceeds a quantity increasing
linearly, quadratically, or (more
generally) as a polynomial function.
CCSS.Math.Content.HSF.LE.B.5
Interpret the parameters in a linear or
exponential function in terms of a
context.
CCSS.Math.Practice.MP3:
Construct viable arguments and critique
the reasoning of others.
CCSS.Math.Practice.MP4:
Model with mathematics.

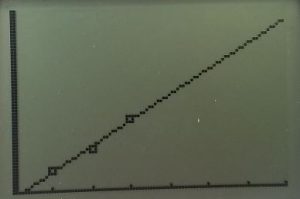
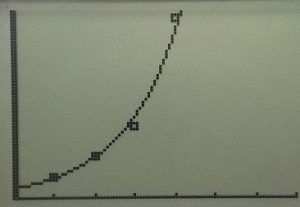

 Learning Target – I will be able to use a motion detector to match and then create a time-distance graph. Represent two numerical variables on a scatter plot and describe any correlation and/or relationship between the two variables.
Learning Target – I will be able to use a motion detector to match and then create a time-distance graph. Represent two numerical variables on a scatter plot and describe any correlation and/or relationship between the two variables.
 and insert the probes inside then they will select the green arrow that will be shown on the bottom left hand corner of the screen to collect the temperatures for both Celsius and Fahrenheit. After 1 minute the students will stop the collecting the data by pressing the red rectangle. Then they will go to the analyze menu and select curve fit. Then they will select the red temperature and then click linear and write down their regression equation on the worksheet handed out to them for Celsius and then repeat for the blue temperature(Fahrenheit). The students who will be in groups of three will compare and contrast these temperatures graph them both on a piece of paper and then form a linear equation for both of the different scales. Then the students will use the information to tell whether the equations are the same, parallel, or intersecting and if they intersect where?
and insert the probes inside then they will select the green arrow that will be shown on the bottom left hand corner of the screen to collect the temperatures for both Celsius and Fahrenheit. After 1 minute the students will stop the collecting the data by pressing the red rectangle. Then they will go to the analyze menu and select curve fit. Then they will select the red temperature and then click linear and write down their regression equation on the worksheet handed out to them for Celsius and then repeat for the blue temperature(Fahrenheit). The students who will be in groups of three will compare and contrast these temperatures graph them both on a piece of paper and then form a linear equation for both of the different scales. Then the students will use the information to tell whether the equations are the same, parallel, or intersecting and if they intersect where?

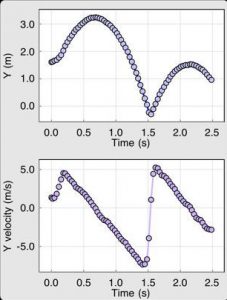
 In this activity students are to use a
In this activity students are to use a