Mathematics History

Post your ideas for integrating math history into your curriculum.

What does common sovereignty mean? (MP3 Math Reasoning)

oursland Common Core State Standards Mathematics, Improve Mathematical Thinking, Mathematics History, Picture Problems

Integrated Mathematics and Social Studies Lesson
th-2The United State Constitution protects tribal sovereignty by Indian Nations but the Indian Nations are not completely sovereign. To understand the interplay between Tribal, Federal, State, and local governments on the Tribal sovereignty read the attached HS_US_L2_Supremacy_Commerce_Clauses_Boldt.

Fishing rights were among the rights protected by treaties for many of the tribes in Northwestern Washington. In 1974 the Boldt decision reaffirmed the “usual and custom” fishing grounds and rights of the treaty tribal (native) people of coastal Washington State.  The Boldt decision was the result of much conflict for many years leading up to the 1970’s, to understand this conflict read the attached HS_US_L1_Constitution_Boldt_Article_Activity.

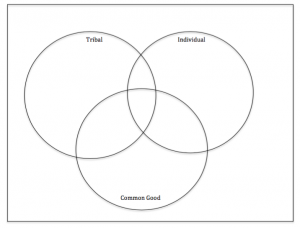
In the Boldt decision, Judge Boldt considered the interaction between individual rights, tribal rights, and the common good [non-tribal people]. A part of the decision was that treaty Indians were entitled to 50 percent of the fish that came to the “usual and accustomed places” because an 1854 treaty used the language “in common with.” The Boldt decision is attached Boldt_Decision.

The ramification of this decision is still very much apart of fishing today in Northwest Washington.  To understand some of the present views read the following  Seattle PI article and history lesson.  In present day legal decisions and ecological activities cooperation is needed to ensure that the number of salmon is increased.

As a math lesson uses your knowledge of Venn diagrams to identify the region of the Venn diagram you feel a current legal or ecological issue should reside. Each student needs to identify at least two issues from one of the three documents and one of personal interested. Write your issue on a posted note and place the note in the region on the Venn diagram you feel this issue should reside. After all students have place three posted notes on their Venn diagram the students will get into groups of four to discuss their claims. The teacher will take notes during the group discussion period and discuss the placement of one issue from each group.  Rubric for the lesson in on the attached worksheet. Venn Diagram Boldt Decision – Impact Issues between individual

Screen Shot 2015-12-11 at 12.41.19 PM

 

Learning through Failure in Mathematics

oursland Mathematics History

Submitted by Michael Jaeger — Saccheri’s great mistake

The history of mathematics is littered with long stretches of failure by bright minds to prove or disprove various propositions. Saccheri provides a great example of why we should avoid allowing our own preconceptions to distract us from deductive logic. Finally, student will be relieved to see that even the brightest minds struggle immensely.

Learning from Euler

oursland Mathematics History

Submitted by David Assink — Konigsberg

There are many names that dominate the world of mathematics, from Euclid to Fermat to Riemann. One name though pervades nearly every eld of study in mathematics, that of Leonhard Euler. Euler is known not only for his innovation and creativity, but also for the sheer volume of high quality work. Within this collection of work we can actually see the informal introduction of a new field of mathematics, the pre-creation if you will of graph theory. Euler, in his paper which appeared in Commentarii Academiae Scientiarum Imperialis Petropolitane, published in 1736, tackles the Bridges of Konigsberg Problem, which can be considered as \the starting point of modern graph theory.”

Use examples from a 2000 year old Chinese textbook

oursland Mathematics History

Aaron Young submitted — ninechapters

The current hot trend in education is using real world examples to teach students mathematical concepts. The days of memorizing tables and plugging and chugging their way through an endless supply of example problems are out of style. Even here, the Chinese have bested our discovery by over 2000 years. Originally published somewhere around 200 B.C., Jiuzhang Suanshu or Nine Chapters on the Mathematical Art, is a tour de force textbook covering a wide range of topics. Is it possible to use this 2000 year old Chinese textbook to teach modern mathematics students?