Author: justinhastings

Slopes of Parallel and Perpendicular Lines HSG.GPE.B.5

justinhastings CCSS-Math Learning Progressions, HS Geometry

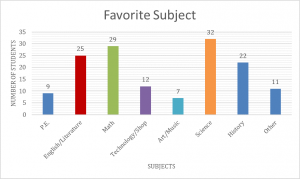
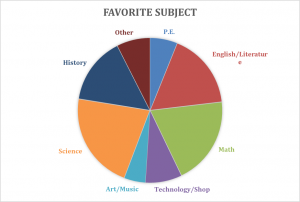
This learning progression is based on the students being able find the slopes of lines and determine if two lines are parallel or perpendicular based on their slopes. It a compilation of three math tasks that will help students understand how to find the slope of a line, classify lines as parallel or perpendicular, and writing equations in slope intercept and point slope forms.

Students will use the slope formula to find the slope a line that is graphed as well as find the slope of a line when two points for a line are given.

  • MATH.CONTENT.HSG.GPE.B.5– Prove the slope criteria for parallel and perpendicular lines and use them to solve geometric problems (e.g., find the equation of a line parallel or perpendicular to a given line that passes through a given point).

Students will be using the slopes of two different lines to determine if they are parallel or perpendicular. They will recognize that parallel lines have the same slope and slopes for perpendicular lines are opposite reciprocals.

  • MATH.CONTENT.HSG.CO.C.9– Prove theorems about lines and angles.

Students will learn to write equations in point slope form and slope intercept form. They will use the information from these equations, as well as knowledge from the previous tasks to graph lines.

  • MATH.CONTENT.HSS.ID.C.7– Interpret the slope (rate of change) and the intercept (constant term) of a linear model in the context of the data.

Formative assessment in the form of observation and discussion will be the primary procedure to support student learning. I will observe how they are finding solutions and ask them questions about their understanding of the learning targets.  At the end of each task students will be given a handout, which will also show how well they are able to meet the learning targets.

Slopes of Parallel and Perpendicular Lines Learning Progression

Proportion and Similarity HSG.SRT.A.2

justinhastings CCSS-Math Learning Progressions, HS Geometry

 

This learning progression is provided to support student’s understanding of ratios and proportionality in relation to similar figures. There is a series of three consecutive math tasks that will be completed by students to help guide them through using ratios and proportions to prove figures are similar.

Students will use their knowledge of algebra to express proper ratios and simplify them correctly. They will also be using the cross product of ratios to solve the proportions.

  • MATH.CONTENT.HSA.SSE.B.3-Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.

Students will identify congruent angles and corresponding sides of a polygon so they can find the similarity ratio. Once they do this, they will be able to recognize the sides and angles that are proportional and determine if polygons are similar.

  • MATH.CONTENT.HSG.SRT.A.2-Given two figures, use the definition of
    similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides.

Students will use triangle similarity theorems to show how congruent angles and corresponding sides that are proportional determine if triangles are similar.

  • MATH.CONTENT.HSG.SRT.A.3-Use the properties of similarity transformations to establish the AA criterion for two triangles to be similar.

Formative assessment in the form of observation and discussion will be the primary procedure to support student learning. I will observe how they are finding solutions and ask them questions about their understanding of the learning targets.  At the end of each task students will be given a handout, which will also show how well they are able to meet the learning targets.

Proportion and Similarity Learning Progression

Creating a Pin on Your Cell Phone HSS.CP.B.9

justinhastings HS Statistics & Probability, Picture Problems

Math Problem- How many different pins can you possibly create on your cell phone using the digits 0-9? How many different pins are possible using any given digit only once?

CCSS Math- HSS.CP.B.9 – (+) Use permutations and combinations to compute probabilities of compound events and solve problems.

This picture will help the students relate creating a pin number for their cell phone to mathematical content. This can be used for a mathematics activity in a statistics course to influence critical thinking and understanding mathematical concepts. By having the students recognize the total number of pins possible will introduce them to more complex ideas that involve permutations and combinations. The teacher can start off the lesson by using less digits and having the students work in groups to discuss and write out all the possible pins. This will actively engage them and stimulate their ability to critically think and solve problems. For further teaching, using a graphing calculator and the alphabet to create passwords can be used also.

What Does the Motion of a Rolling Object Look Like? HSF.IF.B.4

justinhastings Common Core State Standards Mathematics, HS Functions, Technology Teaching Issues

Students can get easily confused when it comes to understanding variables of a graph and visualizing what that information represents. This activity will allow students to see how the path of an object moving toward and away from a given point is modeled. With the use of their TI-84 Plus graphing calculators and the Vernier CBR-2, students in small groups will study the motion of a tennis ball and a toy car rolling up and then back down a ramp. This gives them an opportunity to practice interpreting  the motion of the objects through a hands on activity.

The graphs for the motion of either object should be similar in that they are parabolas, but students will be able to see what determines their properties. At first, they will be asked to visualize and sketch what they imagine the graphs would like. Then by using the technology explained, they can see how their original assumptions compare to the graphs obtained from the motion detector. This will encourage students to critically think about an object in motion and have a better understanding of how its distance from the starting point in relation to time is represented.

Activity Worksheet-Rolling Through Motion

Practice Standard:

CCSS.Math.Practice.MP5- Use appropriate tools strategically

This activity relates to the Common Core State Standard:

CCSS.Math.Content.HSF.IF.B.4
For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship.

Find the Percentage and Angle of Each Subject A.SSE.B.3

justinhastings Assessment of CCSS-Math, HS Algebra

Assessment Task

A survey of 10th grade students was given to determine what their favorite subject is. Use the first graph and find the percentage of students that chose the subject as their favorite. Round the nearest hundredth. (.344=34% or .345=35%). Use that information, with previous knowledge about a circle, and find the central angle that each percent represents in the pie chart.

  • Use this pie chart to label percentages and angles of each piece. (Hint: the pie graph is 360°).

  • After finding the percentage and the angle of each subject, write it as a single proportion and solve for the measure of the central angle. The answer should be in degrees.

 

Find the Percentage and Angle of Each Subject Document with Commentary and Solutions (Here)