Author: naomijohnson2

Creating Problems with Variables 7.EE.B.4, MP 4, W.7.2

naomijohnson2 ML Expressions & Equations, Picture Problems

Creating Linear Problems

By Naomi Johnson

 

 

This lesson will focus on this picture and be used to teach standard 7.EE.B.4. This standard required students to used variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems. The students will solve the equations and figure out the answer to the last problem. We will then discuss how they came to the answers. They will then be given the chance to create their own problems with a system of equations using their own pictures to represent variables in equations. They will then show them to their peers which will show the other students the different cultures and individuality of everyone in class.

This lesson could be an integrated lesson with English Language Arts because the students could then write about their equations, what each picture represents, and why they chose to make them as they did. This lesson could also incorporate the student’s different cultures because they are allowed to use whatever picture they want and it can represent themselves however they would like. The students are given the freedom to bring themselves into the problems, and this includes their individuality and cultures. They can then share these cultures with their peers when they share their problems to the class.

Paper Bridges CCSS 8.EE.B.5 MP 4

naomijohnson2 ML Functions, ML Modeling, Uncategorized

Paper Bridges

Standard: CCSS 8.EE.B.5 MP 4

By: Naomi Johnson, Rachel Van Kopp, Tracy Van Lone, Natasha Smith, and Kimberly Younger

Problem

Paper Bridges is looking at the correlation between the number of pennies that a number of paper bridges could hold. To find this, we folded pieces of paper that were all the same size in the same way. We then put one paper, folded as a bridge, on two equal size books, an inch of paper was on each book. We then placed pennies on the bridge until it caved in 1/8 of an inch or collapsed, whichever came first. We then counted the pennies and recorded the number.

We repeated these steps with 2, 3, 4, and 5 paper bridges laying on top of each other to see how more paper effected the number of pennies that were able to be help.

Analysis

Table 1: Data collected from our experiment.

To analyze our data, we inputted the data from Table 1 into our calculators. We performed a linear regression on the data as well as an exponential regression. We were given the following equations:

Linear Equation: y = 12x – 2.2

Exponential Equation: y = 5.9259 * 1.6537^x

We plotted all our data and graphed our equations. Figure 1 shows what this looked like.

Figure 1: Our data plotted with our two equations. The red line represents the linear equation and the blue line represents the exponential equation.

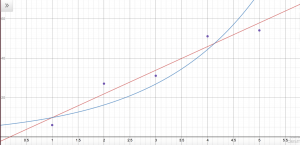
After looking over Figure 1, we had a hard time determining which equation did a better job of representing our data. Neither line was incredibly close or far away from the points. At this point in time, we believed both equations could possibly be good representations of the data.

We decided to find the absolute value of the difference between each data point and their expected linear and exponential value. We then averaged the differences. Table 2 shows what we found.

Table 2: The absolute value of the difference between each data point and their expected linear and exponential value. In the bottom line is the average of the differences.

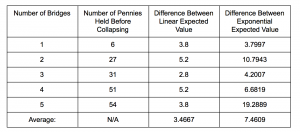
We were than able to see that the linear equation seemed to better match our data. All the linear differences compared to the exponential differences were smaller expect for with the first data point. The average exponential difference was more than two times the average linear difference. It appeared that the exponential equation could be growing too fast.

While we may have found reason to believe the linear equation was the better fit, we still felt like we needed more data. When doing this activity in a classroom, we would recommend extending the domain and creating more data points. We would also recommend having students do multiple trials of the experiment or having students share their data with the class.

Extension

A lot of variables come into play when a structure collapses. For instance, our paper bridges collapse as more and more pennies are placed in the middle. Interestingly, even though all groups of students involved in the investigation in our class used the same paper, folded the same way, and collapsed their bridges with pennies weighing exactly the same amount, no two teams’ bridges collapsed under the same number of pennies. Some teams gently “placed” their coins on their bridges, enabling their bridge to hold more weight than the teams that “dropped” their coins on the bridges. Some teams spread their coins a bit wider along the center of their bridge than others, enabling more coins to stack up on their bridge prior to its collapse. Other teams folded their bridge papers more sharply and precisely, causing the structure to be more rigid. Many variables add up to change the dynamics from one bridge to another despite seemingly identical bridge designs and project execution instructions.

A real-life structural collapse occurred on 1987 when UW built an addition to Husky Stadium. Nine temporary guy wires were holding the stadium roof up while additional structure was built underneath. The stadium was well designed and should not have collapsed. But a collection of variables added up to change the dynamics from the stadium addition as designed to the stadium addition as executed. Construction specifications were not very specific about when the appropriate time would be to remove the temporary guy wires and how many should be removed at a time. Ask students to read these articles and identify the variables they see impacting the collapse. Would the structure have stood if only 5 guy wires had been cut? What if only 4 guy wires were cut and the hollow steel tubular beams had been filled with concrete as specified by the designer? Would the stadium have stood? What about the cat?

Husky Stadium history

Husky Stadium Failures

 

SaveSave

SaveSave

SaveSave

SaveSave

SaveSave

SaveSaveSaveSave

Circles and Squares 7.RP.2.a, 7.G.A.1, and 7.G.B.4 MP 4

naomijohnson2 ML Modeling, ML Ratios & Proportional Relationships

Circles and Squares

Standard: CCSS.7.RP.2.a CCSS7.G.A.1 CCSS.7.G.B.4 Math Practice 4

By: Naomi Johnson, Rachel Van Kopp, Tracy Van Lone, Natasha Smith, and Kimberly Younger

The problem:

This problem was based on Circle-Square by Dan Meyer and had a circle and a square on a line that moved together. When one shape grew, the other would shrink by the same amount. Our job was to find out when the two shapes would be equal in area.

Connections/Solution:

We found that when the perimeter of the square is 21.1 and the circumference of the circle was 18.9, then the areas would be equal to each other. After finding the areas, we noticed that the equations for the two were very similar. The area for the square was A = 28.4234 and the area of the circles was A = 28.4234, so the square was divided by 16 and the circle was divided by 12.567, so the radius of the circle and the distance from a corner to the center of the square will be very close. Another connection that we noticed was that their perimeter and circumference will always equal 40 because that was the length of the number line it was on.


 

Extensions:

  1. Have the circle and square not touch, and looking at how that might change the perimeter and circumference. They could also extend the number line from 40 to 60 or beyond and looking at the impact that would have. For discussions, the teachers could have the students think about what would happen if, instead of the two shapes moving together, they moved apart from each other.
  2. Use a cube and sphere instead of a circle and square:

    Sphere & Cube Dimensional Relationship Exploration

    What are the dimensions of a cube and a sphere of equal volume?
    What are the dimensions of a cube and a sphere of equal surface area?
    Are there any cool relationships between the dimensions of the cube and the sphere?
    Which cube dimension most closely resembles the sphere’s radius? Why?
    Use these calculators to analyze the relationships:
    Cube: https://www.geogebra.org/m/g6ffapbP    Sphere: https://www.geogebra.org/m/Xyc8W4Qn

(Note: The sphere radius illustrated above is 1/phi. The cube edge is 1.)