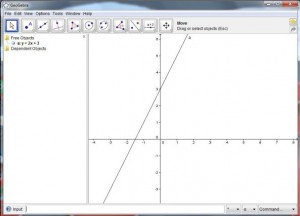
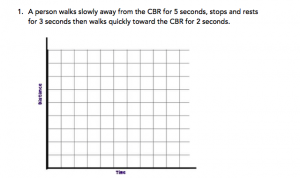
Imagine you are walking to class and you see your friend up ahead so you run to catch up with him. Can you model this situation mathematically? Of course you can! Assuming that you and your friend are moving at constant speeds, you can set up a system of linear equations. You can model this graphically by plotting distance versus time. If you were to plot the lines on the same set of axes, the point where the two lines cross would represent the physical location where you passed your friend.
Imagine you are walking to class and you see your friend up ahead so you run to catch up with him. Can you model this situation mathematically? Of course you can! Assuming that you and your friend are moving at constant speeds, you can set up a system of linear equations. You can model this graphically by plotting distance versus time. If you were to plot the lines on the same set of axes, the point where the two lines cross would represent the physical location where you passed your friend.
It is possible to create models for situations like this in the classroom using Vernier CBR2 Motion Detectors.
In the Hey! Wait Up! activity, students will work in groups of four: 2 people will be the walkers, 1 person will start the motion detector and operate the stopwatch, and 1 person will mark the point where the walkers intersect. Each group will work together to collect and analyze motion data in order to determine the solution to a linear system of equations using a graphing calculator. They will then check this solution by creating a system of linear equations and solving it by hand. This activity is best done after the students have been introduced to systems of linear equations and how to solve them.
To complete the The Hey! Wait Up! activity each group will need 2 Vernier CBR2 Motion Detectors (with appropriate cables), a TI83 or TI84 calculator, a meter stick, and a stopwatch.
This lesson aligns with the following Common Core State Standards:
CCSS.MATH.CONTENT.8.EE.C.8– Analyze and solve pairs of simultaneous linear equations.
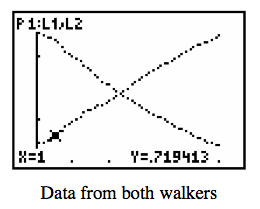 Students will be using the calculator results to find the coordinates of two points for both lines which they will then use to find the slopes of each line. Students will also use the calculator results to find the y-intercept of each line. Using this information, students will be able to create equations for the lines that they will then use to make a system of linear equations and solve.
Students will be using the calculator results to find the coordinates of two points for both lines which they will then use to find the slopes of each line. Students will also use the calculator results to find the y-intercept of each line. Using this information, students will be able to create equations for the lines that they will then use to make a system of linear equations and solve.
CCSS.MATH.CONTENT.8.EE.C.8.A– Understand that solutions to a system of two linear equations in two variables correspond to points of intersection of their graphs, because points of intersection satisfy both equations simultaneously.
At the end of this activity, students will be able to connect that the point where they crossed when walking is the point where the two lines intersect and that this coordinate point is the solution to the system of linear equations.
To conclude this activity, students will be given an exit slip that asks:
- In your own words, what is a system of linear equations?
- Give me an example of a real world situation (that does not involve walking/ running) that you could model using a system of linear equations.
From this you can determine and gauge your students’ conceptual understanding as well as see if they can apply the idea of using systems of linear equations to model other everyday experiences.
A benefit of using Vernier Motion Detectors when teaching the concept of systems of linear equations is that it makes the concept personal for the students. It helps bring mathematics out of the classroom and into the real world. Rather than seeing the systems of linear equations as just lines on the graph, they can see that in this situation those lines represent something, namely the students’ walks. This activity also gets the students involved in their own learning by having them get up and move around when they are doing the walking activities and collecting the data. This makes the data concrete for them rather than just some numbers, equations, and coordinates they have to work with in order to find a solution.
A Vernier CBR2 Motion Detector costs $99. To buy or to find out more about the Vernier CBR2 Motion Detector visit http://www.vernier.com/products/sensors/motion-detectors/cbr2/
To find out more about Vernier Software & Technology and explore their other products visit http://www.vernier.com/
Hey! Wait Up! worksheet: Hey! Wait Up!-Systems of Linear Equations with Vernier Motion Detectors



 Students work in groups of four: a. one person walks, b. another operates the calculator, c. another draws the graph on the calculator, and d. the graph of the peers walk, and the final person gives and writes the walking directions. On the next walk the students switch tasks, so that everyone performs all tasks.
Students work in groups of four: a. one person walks, b. another operates the calculator, c. another draws the graph on the calculator, and d. the graph of the peers walk, and the final person gives and writes the walking directions. On the next walk the students switch tasks, so that everyone performs all tasks.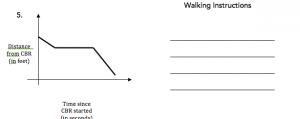
 TI- 83 or 84
TI- 83 or 84




 Pushing this opens a new menu that has more options in the upper right hand corner called Mode, and just wait there’s more. If you push the Mode button it opens? Yep, you guessed it, another menu with more feature!
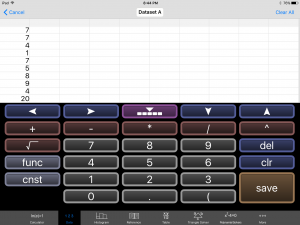
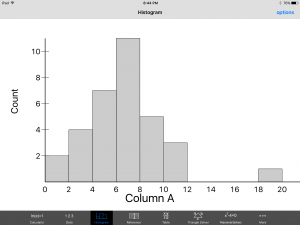
Pushing this opens a new menu that has more options in the upper right hand corner called Mode, and just wait there’s more. If you push the Mode button it opens? Yep, you guessed it, another menu with more feature!  This time click the Statistics option and hear that ‘click’ sound play your favorite tune. ‘Click.’ Now don’t go away, if you place your order today we will throw in, for absolutely free, that’s right, absolutely free data set entry into a spread sheet. Just enter your data set. Then here comes my favorite part, are your ready? Click the Histogram button at the bottom of the screen and ‘presto’, your histogram has been summoned. Turn every student in your class into a Mathamagician. That’s right! A Mathamagicaian, and bring your lessons to life. And if you order your copy of GraCalc between now and Armageddon, I’ll cut the cost in HALF. That’s right, In half. Not good enough, you say? Well finish reading this blog and I let you have the app for my famous low, low, super duper, can’t get a better deal anywhere price of… are your ready? FREE, Yes I said it, Freeeeeeeeeeeeeeeeeeeeeeee.
This time click the Statistics option and hear that ‘click’ sound play your favorite tune. ‘Click.’ Now don’t go away, if you place your order today we will throw in, for absolutely free, that’s right, absolutely free data set entry into a spread sheet. Just enter your data set. Then here comes my favorite part, are your ready? Click the Histogram button at the bottom of the screen and ‘presto’, your histogram has been summoned. Turn every student in your class into a Mathamagician. That’s right! A Mathamagicaian, and bring your lessons to life. And if you order your copy of GraCalc between now and Armageddon, I’ll cut the cost in HALF. That’s right, In half. Not good enough, you say? Well finish reading this blog and I let you have the app for my famous low, low, super duper, can’t get a better deal anywhere price of… are your ready? FREE, Yes I said it, Freeeeeeeeeeeeeeeeeeeeeeee.